コンプリート！ 順列 と 組み合わせ 464862-順列 と 組み合わせ

例えば，順列では， (A，B)と (B，A)は違うものになりますが，組み合わせでは同じものを表していることになります。 数学的には，４個のものから３個取り出して並べる順列の数は， ４ P ３ ＝４×３×２＝２４となります。つまり、 順列では、並べる順序を問題にして考えますが、組合せでは順序を 問題にしないで取り出し方だけを問題 にして考えます。 したがって、順序が問題になる取り出し方の場合は順列で、順序が問題に ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ順列と組合せ 順列とは，互いに区別で きるものを1列に並べる ときの並べ方の数，組合 せは，互いに区別できる ものから何個か取り出す ときの取り出し方の数を 言う．

場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

順列 と 組み合わせ

順列 と 組み合わせ-T：「これを順列といい、5P3と書くことにします」 授業例3（組合せ） T：「5色のロケットから3色を選んでつなぐ順列は何通りでしたか？」 S：「5P3 T：「では、5色のロケットから3色を選ぶだけの場合とどちらが一致しやすいと思いますか？ 組み合わせ論とは、複数の要素が取りえる方法について考えることです。 についてまとめています。 順列（階乗）は、 ある数の要素を並べるときの数を示す 。 初めに入る数字nからn1,n2の数字を並べ、値をかけていきます。 1人、2人と並べていくたびに、 取りえる選択肢は少なくなっていく 。 順列とは、 ある数から要素を選んでそれを並べることをいい ます

順列と組合せの違いってなんでしょうか 調べてもあまりよくわからないです Clear

10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを取って並べる順列 10 P 2 =10·9=90 のうち，先頭が0のもの（9個）は1桁になるから，909=81個 （別解） 十の位は0以外の9通り，それぞれ1の位は9通りだから，9×9=81通り 例 2桁の整数の総数 （解答） 10個の数字 0,1,2,3,4,5,6,7,8,9 から重複を許して2つを取って並べる順列 10Π2 =10 2 =100 のうち，先頭が0のもの（10個）は1桁になるか順列、組み合わせ、二項定理 数学についてのwebノート ・定義： 順列 ・ 組み合せ ・定理： 組合せの性質 ・ 二項定理 ・ 多項定理 ※ 総目次例 2桁の整数の総数 （解答） 10個の数字 0,1,2,3,4,5,6,7,8,9 から重複を許して2つを取って並べる順列 10Π2=102=100 のうち，先頭が0のもの（10個）は1桁になるから，=90個 （別解） 十の位は0以外の9通り，それぞれ1の位は10通りだから90通り 同じものがある

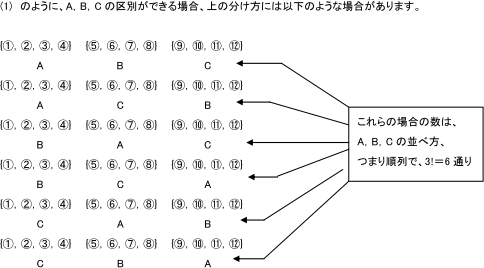
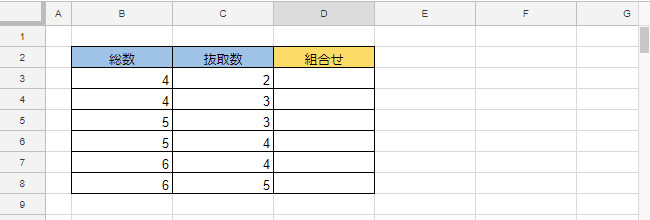
組み合わせは、順序に意味がある順列とは異なります。 総数 = n、抜き取り数 = r とすると、組み合わせの総数は、次の数式で表されます。 問題3それぞれA,B,Cと書かれたカードがあります。数学・算数 順列・組み合わせ いつもお世話になっております。 高校1年生の者です。 テスト前のためずっと勉強をしているのですが、 数学の順列・組み合わせでわからない問題があります。 問 3人乗 質問No世界大百科事典 第2版 順列･組合せの用語解説 n個の互いに区別のつくものからr個取って，ある順序に並べたものを順列という。そのような並べ方，すなわちn個のものからr個を取った順列が全部でいくとおりあるかは，で与えられる。また，異なるn個のものからr個を取り出し順序は考え

今回から 「順列」の場合の数 について学習しよう。 「順列」とは、漢字が表す通り 「順番をつけて並べる」 ということ。順番をつけて並べる場合の数 は、とても重要なテーマで、様々なパターンの問題があるんだ。 これから計10回にわたって、順列の問題のパターン別解法を説明していくよ。 ①は 順列 で、答えは 5 P 2 ＝5×4＝通り ②は 組み合わせ で、答えは 5 C 2 ＝5×4÷2＝10通りになります。順列・組合せの問題に挑戦！ 順列・組合せの問題は、確率論、計算数学、オートマトンの理論および数理経済学において きわめて重要である。しかし、現行の教育課程においては、深く考えさせる問題が少なく、十 分な訓練ができる状況にはない。

順列と組合せの違いとその公式とは 応用問題５選もあわせて解説 遊ぶ数学

同じものを含む順列と組合せは 同じ です 問題４選もあわせて解説 遊ぶ数学

順列と組合せの違いとは順番の「区別」があるかないかです 結論を一言でまとめると 順番の「区別」がある → 順列;前回 https//wwwyoutubecom/watch?v=gkeQK_kfa5w 次回 https//wwwyoutubecom/watch?v=4LJtn7VG67Mサブチャンネル とある男がゲームを順列、組み合わせ、円、重複、組分け。これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列 7個のガラス玉から3個選んで一列に並べる $_7p_3$ 組み合わせ

3right 76 Defense 74 Descubre Como Resolverlo En Qanda

順列pと組み合わせcの違いと 簡単 な見分け方

 18年6月29日 21年1月22日 SPI の 組み合わせにおける順列の問題 です。 推論の順列とは違い、 並べるパターンが何通りあるか を主に問われます。 目次 1 例題1 11 問題1順列･組合せ総合問題 練習問題19 5人の旅客が3件の旅館に泊まる泊まり方は何通りあるか。 ただし1人も宿泊しない旅館があってもよいとする。 上の問題において，人を仮に固定し，どの旅館に宿泊するか，ということを考えればよいのです。 発想の 順列と組み合わせの違いは、選び出した／取り出したものの 並び順を考慮するかどうか です。 「順列」は取り出したものの 並び順を考慮 しますが、「組み合わせ」では 並び順を考慮し

数学iaiib全問題 Ia 場合の数 確率

区別がない組分け 数学 苦手解決q A 進研ゼミ高校講座

A11 順列、組み合わせ、重複組合わせ 本節では 重複順列以外に高校数学でも馴染みの深い「順列」、「組み合わせ」、「重複組み合わせ」といった概念を Mathematica を用いて吟味する。 1 順列 まずオブジェクト、 "bn,k"、を構築する。これは、「異なるn個のものから重複を許さずk個を 今回の記事では、順列・組み合わせを求める際に使用します。 itertoolsのインストール方法 itertoolsはPythonの標準ライブラリなのでインストールの必要はありません。 順列 順列とは、異なるn個の中から k 個を順番をつけて並べる場合の並べ方です。 SPI 場合の数 順列・組み合わせの基礎 この単元の基礎は分量が多いです。 頑張って学習しましょう！ ！ 1 PとCの使い分けの解説です。 ＜問題＞ 1~3のカードが1枚ずつある ① 2けたの整数は何通りできるか ② 2枚選ぶのは何通りあるか

Spi 数学 対策問題 組み合わせ 円順列 しかくのいろは

Permut 順列の組合せの数を求める スプレッドシート関数

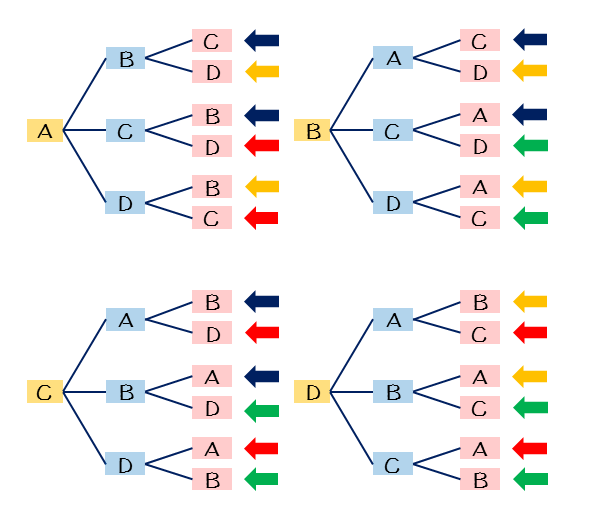
順列・組合せじゅんれつくみあわせ n 個の異なるものから r 個を取り出して1列に並べたものを n 個から r 個とる順列といい、その総数を nPr と書く（ P は、順列の英語permutationの頭文字をとったもの）。 たとえば、4個の文字A、B、C、Dから3個をとって並べると、次のような24通りの順列ができる。 したがって、 4P3 ＝24である。順列、組み合わせ、円、重複、組分け。これらの場合の数の違いとその見分け方を簡単に解説します。 ここでは共通の例として、7個のガラス玉があった場合を考えてみます。 順列 7個のガラス玉から2節 順列 8時間（本時は6／8、7／8） ⑥ 本時の題材 同じものを含む順列 ⑦ 本時のねらい 同じものを含む順列について、異なるものを並べる順列との違いを理解し、公式を導き、問題 を解けるようにす

場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

順列と組み合わせ 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

 今回は順列と組み合わせについて アウトプットしていきます。 この先、分布について計算する為には 順列と組み合わせの式を使うケースが ありますが順列と組み合わせの理解が なければ何の計算をしているか分から なくなりますので今回しっかり学んで いきましょう。異なる n個のものから 重複を許して r個を選ぶ組み合わせの総数を求めます。 重複組合せ（表） 異なる n個のものから、重複を許して r個を選ぶ組み合わせの総数の rを変化させた表を求めます。 順列 異なる n個のものから r個を選んで並べる順列の総数 nPr を求めます。 順列（表） 異なる n個のものから r個を選んで並べる順列の総数 nPr の rを変化させた表を求め組合せ 一日1440分ある時刻から任意で12個抽出すると何通りあるかを調べた。 一日12本しか列車が来ないローカル線の駅の時刻表を見て、ふと思いついた。 桁数がとてつもなく多くて驚いた。 ポーカーをやるっているときにポーカーの手は何通りあるのか

順列と組み合わせの関係 楽しく学ぶ大学受験数学

ときわ台学 統計学 順列組み合わせ

 順列・組み合わせ・階乗とは わかりやすくまとめてみた数学 普段生活している上ではなかなか出会う機会がなかったのですが、 最近よく目にするようになった、 『機械学習』 『統計学』 『メディアアート』 など様々な分野で、 『順列』や『組み合わせ』はたっぷり組み込まれているようで。 アオキ同じものを含む順列の公式を用いた問題 同じものを含む順列文字列 同じものを含む数字を並べてできる整数（偶数） 最短経路; JavaScriptで"順列"と"組み合わせ"の説明ですがとてもわかりやすいです。 再帰処理で求める順列(nPr)JavaScript Qiita この記事について プログラミングクイズを解くにあたり、再帰処理を使うとスラッと解けそうな気がする問題がいくつかありま qiitacom 順列とは 異なる n 個のものの中から r 個

順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス

順列 組み合わせ 階乗とは わかりやすくまとめてみた 数学 もんプロ 問題発見と解決のためのプログラミング

 同じものを含む順列 例 a5個、b3個、c2個の合計10個の文字をすべて1列に並べる順列の総数 考え方1同じ文字の位置を選ぶ 先頭から最後尾まで10個の場所からaを置く位置を5つ選ぶ 10 C 5 のこりの場所からbを置く位置を3つ選ぶ 5 C 3 のこりの場所からcを

9 3 確率の計算 順列 組み合わせ 統計学の時間 統計web

基礎力完成 確率 順列と組合せ 短期速習 大学入試過去問シリーズ 数学 1 旺文社 本 通販 Amazon

重複順列と重複組み合わせの問題はどうやって見分ければいいですか Clear

高校数学a 最短の道順の求め方 映像授業のtry It トライイット

動画で解説 数学講座 順列と組み合わせのちがい ふじい塾 English Mathematics

順列と組合せの違いってなんでしょうか 調べてもあまりよくわからないです Clear

場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

順列 組み合わせ Npr Ncr 優技録

順列 組合せ記号 Pukiwiki

数列 順列 組み合わせ計算機 On The App Store

順列 組合せの覚書

高校数学a Npr と Ncr の使い分け 練習編 映像授業のtry It トライイット

順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス

順列と組み合わせの違いとは そしてそれぞれの意味を0から解説

順列と組み合わせ Alis

場合の数 組合せについて 日々是鍛錬 ひびこれたんれん

順列と組合せの違いは 公式は暗記ではなく意味で理解する Aiコトハジメ

同じものを含む順列の問題 京極一樹の数学塾

順列と組み合わせの公式とその違い 問題付き 理系ラボ

組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門

順列のtwitterイラスト検索結果

数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube

順列と組み合わせ 物流業界の歩き方

Q Tbn And9gcqlkpuj7zhs7go Udfrxynu2zb3e4a M8wf5quoql9k Syuaqyl Usqp Cau

数学 P と C の 違い 確率の問題で コンビネーション C とパーミテーション P の違いを教えてください Amp Petmd Com

順列と組み合わせの公式とその違い 問題付き 理系ラボ

Excelを使った数値計算ツールsuitexl

順列と組み合わせの公式とその違い 問題付き 理系ラボ

高校数学a 組合せの計算1 Ncr 例題編 映像授業のtry It トライイット

順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ

重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ

順列と組み合わせの公式とその違い 問題付き 理系ラボ

組合せ Pukiwiki

数学a 順列と組み合わせの違い 無料問題付き 平野雅人のブログ

ほのぼの数学頑張ろう 13年センター試験数学i A 第４問

数学を分かりやすく考えてみようと試みるサイト 分かりやすい高校数学 確率 8 組み合わせ

数学ａ 順列と組合せの使い分けとコツ 教科書より詳しい高校数学

順列と組合せの違いと例題 高校数学の美しい物語

ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun

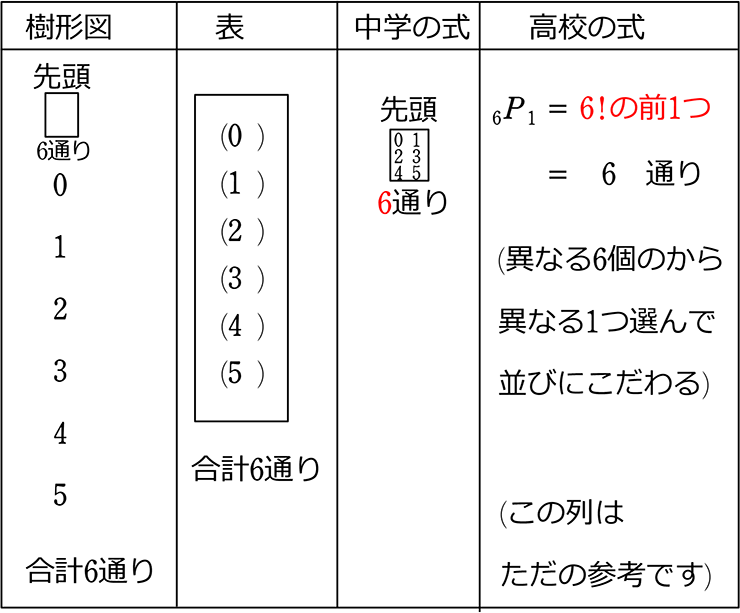
中学数学 場合の数

北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭

Ubu Vu5drjauxm

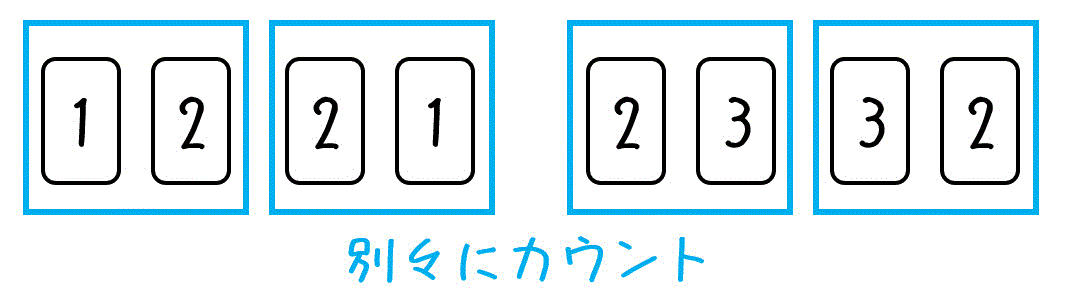
うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾

順列と組み合わせ 算数用語集

順列と組み合わせの公式とその違い 問題付き 理系ラボ

数列 順列 組み合わせ計算機 On The App Store

重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear

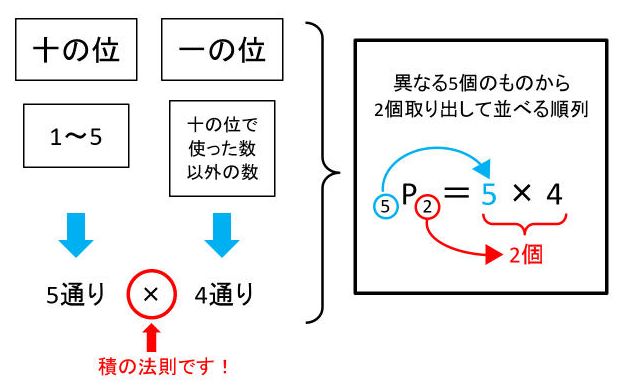
何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ

基本問題 場合の数6 同じものを含む順列と重複組み合わせ 同じものを含む順列 道順 No Youtube

Q Tbn And9gctdg7qzyj8jefiumjmojygwqcr6bhmbi685zwhir13rni5bkqx6 Usqp Cau

Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b

重複順列 Itパスポート出題テーマ別過去問題 平成24年度秋期 テクノロジ系 問78

Pythonで順列と組み合わせ Qiita

順列と組み合わせ をclasspad Netで自動計算 Mathapp Days

なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ

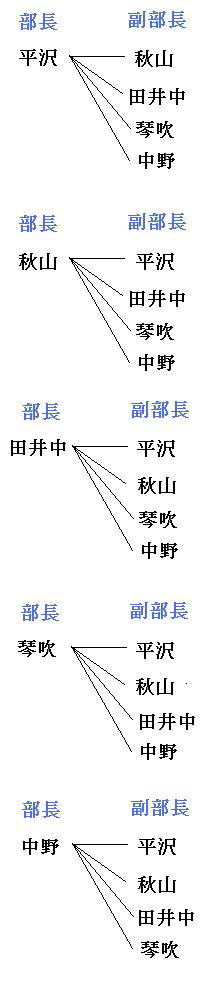
組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ

順列と組み合わせの公式とその違い 問題付き 理系ラボ

Permutation And Combination 順列と組み合わせ Math In English 13 Okenavi

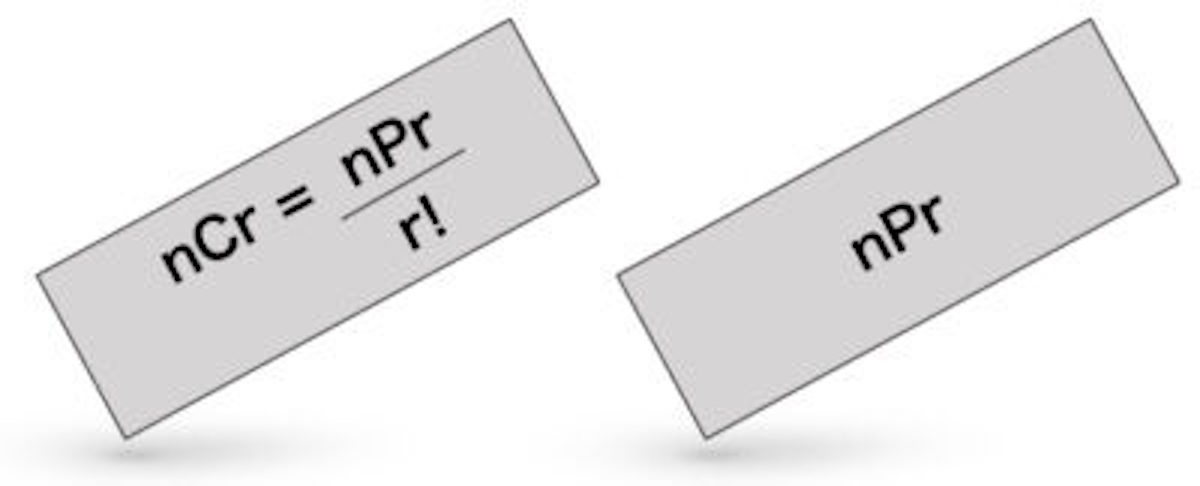
組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather

重複順列と重複を許して取る組み合わせの違い がよく分かりません お願いします Clear

場合の数 組合せについて 日々是鍛錬 ひびこれたんれん

No 2 順列と組合せ

場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート

統計学 順列と組み合わせ Rとpython いっかくのデータサイエンティストをいく

組み合わせ C とは 公式や計算方法 は何通り 受験辞典

順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典

高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ

場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ

48s96ub7b0z5f Net Onajimono Junretsu

3

北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭

順列と組み合わせの最短距離についてこの問題の解説お願いします 問題が Yahoo 知恵袋

場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル ｓｐｉ 空間把握 解いてみてください

同じものを含む順列の問題 京極一樹の数学塾

高校数学a 組合せの活用4 少なくとも 映像授業のtry It トライイット

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

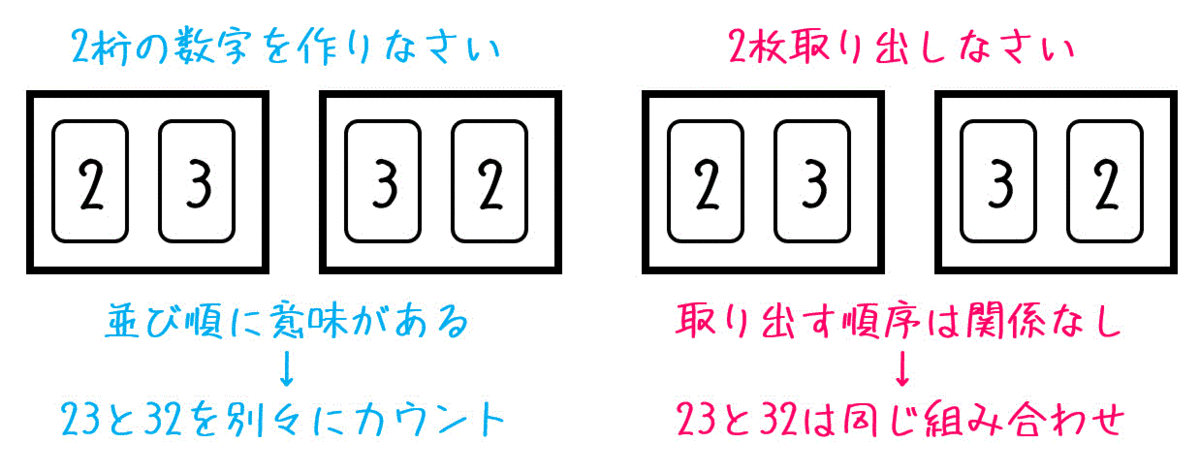
うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾

Excel エクセルで順列と組み合わせの計算を行う方法 場合の数

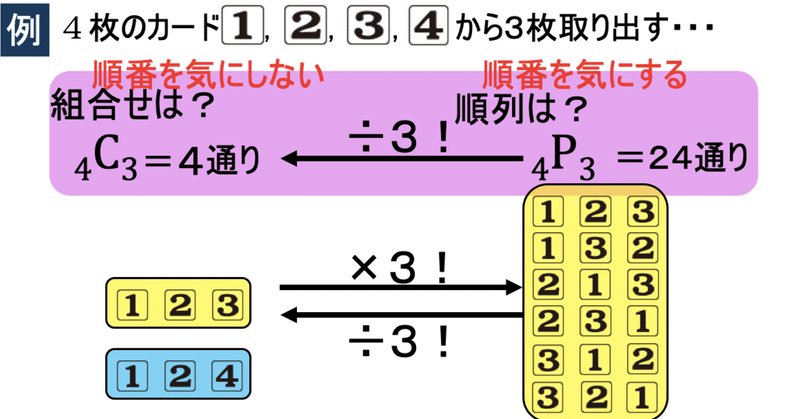
組合せの計算の導入 順列との違い Root Note

数列 順列 組み合わせ計算機 By Yoshiaki Onishi

場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん

機械学習の統計学 順列と組み合わせって何 ししまる みらいのクルマをつくる人 Note

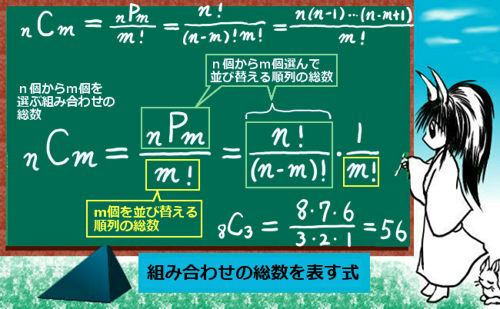
組み合わせの総数 場合の数 理数系無料オンライン学習 Kori

順列と組み合わせの解答 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

Permut関数で順列の数を求める Excel関数 できるネット

Pythonで階乗 順列 組み合わせを計算 生成 Note Nkmk Me

Q Tbn And9gcqlkpuj7zhs7go Udfrxynu2zb3e4a M8wf5quoql9k Syuaqyl Usqp Cau

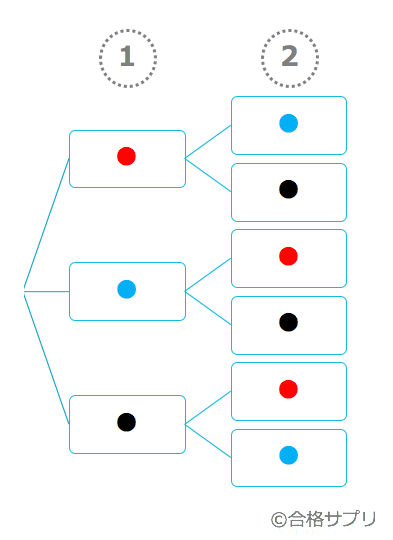
3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ

順列 組合せに頼らない 素朴に数える ための3本柱 わが子を算数 数学嫌いにさせない習慣 朝日新聞edua

Incoming Term: 順列 と 組み合わせ,